可视化

更新: 2021-01-10 14:00:32

1 可视化定义，与图形学、数据挖挖掘的关系

课件：vis-intro-2020-0911

关于定义：

Tamara Munzner 2011: "Computer-based visualization systems provide visusal representations of datasets intended to help people carry out some task more effectively."

大致翻译：提供数据的呈现，帮助人类更有效率的产出。

不同领域的一些输入输出的比较：

input	output	Research Area
Image	Image	Image Processing
Image	3D Model	Computer Vision
3D Model	Image	Computer Graphics
Data	Image	Visualization

关于异同，一些未整理的理解：

数据可视化的目的，是要对数据进行可视化处理，以使得能够明确地、有效地传递信息。
数据可视分析和数据挖掘的目标都是从数据中获取信息与知识，但是手段不同。
数据可视分析是将数据呈现给用户以易于感知的图形符号，让用户交互地理解数据。数据挖掘是通过计算机自动或者半自动地获取数据隐藏的知识，并将获取的知识直接给予用户。
也就是说，数据可视化可以看到交互界面，更适合于探索性地分析数据。而数据挖掘面对的是一堆活生生但黑不溜秋的数据，需要像挖矿一样从中发现金子。
数据挖掘指从一堆数据中挖掘有价值的信息，数据可视化是把数据通过图形画的方式展现出来，让用户更加直观的感受到数据的分布和一些其他信息。所以数据可视化可以用作数据挖掘分析结果的展现方式。

其他拓展类型的可视化：

Scientific Visualization 科学可视化：Scientific visualization focuses on the use of computer graphics to create visual images which aid in understanding of complex, often massive numerical representation of scientific concepts or results. 通常是科学概念和大量数据。
Information visualization: is the communication of abstract data through the use of interactive visual interfaces. 更像是整个信息的输出，比如拿破仑当年路线的那个经典图。
Visual Analytics 可视分析：is the sience of analytical resoning facilitated by visual interactive interfaces - keep human in the loop. 另一种定义：Visual analytics combines automated analysis techniques with interactive visualizations for an effective understanding, reasoning and decision making on the basis of very large and complex data sets. 感觉是人与自动分析的结合来处理更复杂的数据集，需要有interface。

这一章的总结：

可视化的定义
Information visualization、Scientific Visualization 的定义、关注什么样的数据
上面Research Area以及各学科的区别

2 辛普森悖论 boxplots

Simpson's Paradox 辛普森悖论

失势

产生的原因，每个分组的权重不同。

悖论

斯坦福讲义里的例子：某大学历史系和地理系招生，共有13男13女报名。历史系5男报名录取1男，8女报名录取2女。地理系8男报名录取6男，5女报名录取4女。
历史系：1/5（男） < 2/8 （女）
地理系：6/8（男） < 4/5 （女）
合计：7/13（男）> 6/13 （女）
上面的数据给出一个令人迷惑的结论：尽管每个系女生的录取率都更高，但整体算下来男生的录取率却更高。

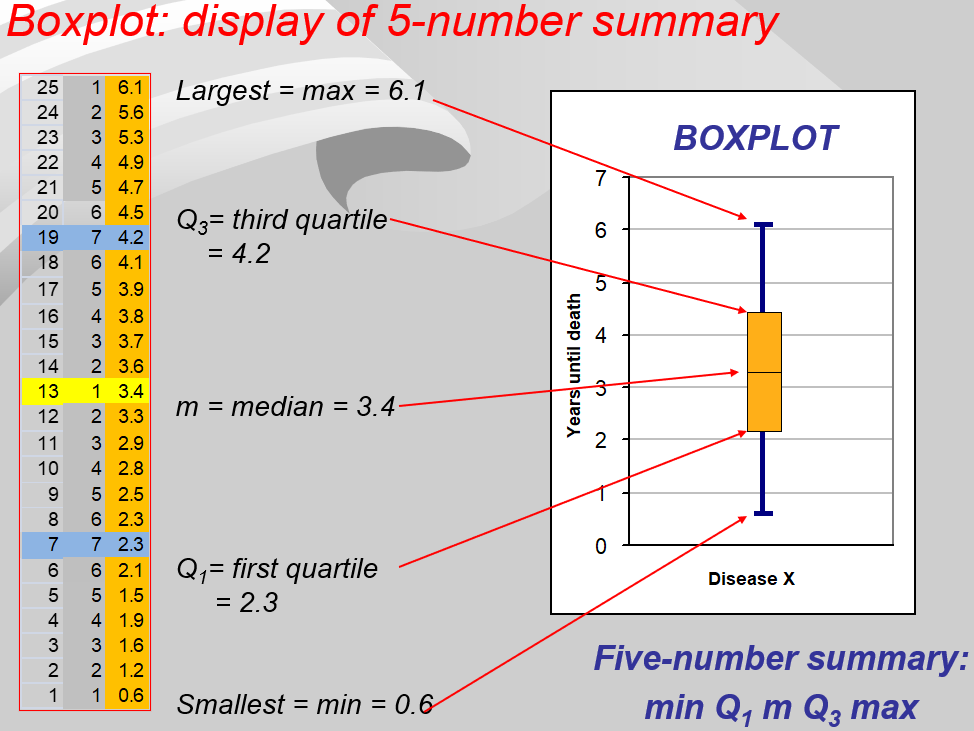
① 计算四分位数 Q1、Q2、Q3，计算公式为 $ Q_i = 1+i*(n-1)/4 $ 其中 Q2=m=中位数，n为数据个数，算出来是数据的位置。如果不是整数，如2.75，则用0.25*[2]+0.75*[3]，[x]表示第x位置上的数。

注意
四分位数位置的计算方法通常有两种（实际维基百科给了4种），这里以0.25处为例
第一种是 (n+1)/4，第二种是 1+(n-1)/4
为什么有多种呢？对于是否包含25%处的点的规定不同、对于如何离散值应该划分区间的范围规则不同…
第一种，为什么是n+1，实际n个数将空间分为了n+1个，若假设总体落在每个区间的概率相同。第二种最好理解，比如 1 2 3 4 5 6 7，则1就是最左端，7就是最右端，则区间实际上是被分成了6块，所以是n-1，然后+1是弥补1之间的序号，需要从0开始数才是正确的位置。
Excel中有两种计算方式分别对应第一种和第二种，，课件上使用的第二种，d3中使用的第二种。

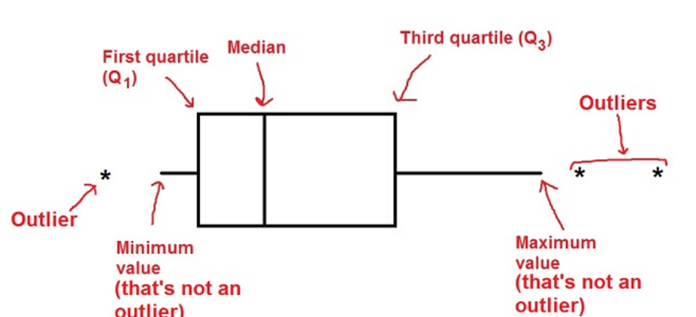
② 计算IPQ = Q3-Q1，则数据的非异常最大值和最小值分别为Q3+1.5IPQ，Q1-1.5IPQ，超过这两个范围的均为异常值。

- 最大值区间： Q3+1.5ΔQ
- 最小值区间： Q1-1.5ΔQ

最大值与最小值产生于这个区间。区间外的值被视为outlier显示在图上.

③ 画线时画出非异常范围内的最大值、最小值、Q1、Q2、Q3。

对于端点的横线，有画的也有没画的，个人建议不画。

可以看的参考：
https://zh.wikipedia.org/wiki/%E7%AE%B1%E5%BD%A2%E5%9C%96
d3 template 的 basic 图形似乎有错误，=+*
https://en.wikipedia.org/wiki/Quartile
一个很有启发但是好像不太对的 csdn：https://blog.csdn.net/weixin_53711329/article/details/111936160

3 平行坐标系

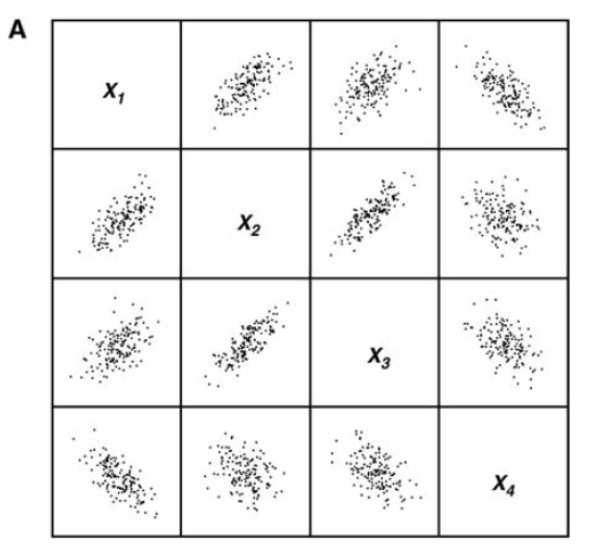
需要掌握：散点图矩阵和平行坐标系的绘制

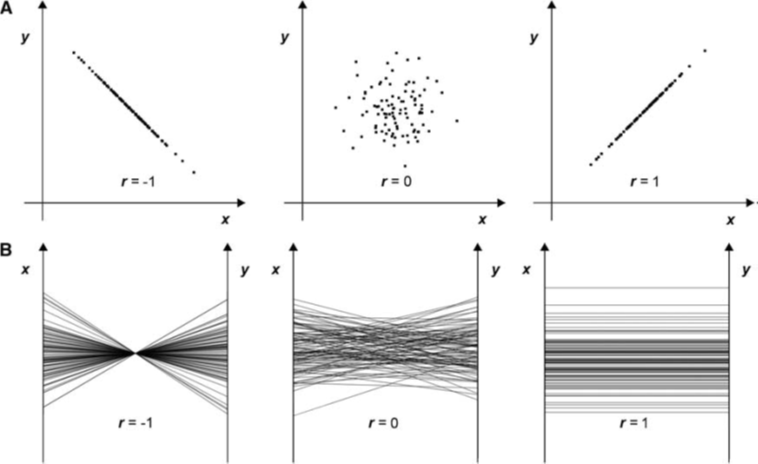
主要下面这三种，注意再多观察一下图1对应之间的关系，比如反比例对应成一个点之类的。

第二张图是对称的，但是如果x过于多，那么会画太多的图了，所以才可以用图3来代替。

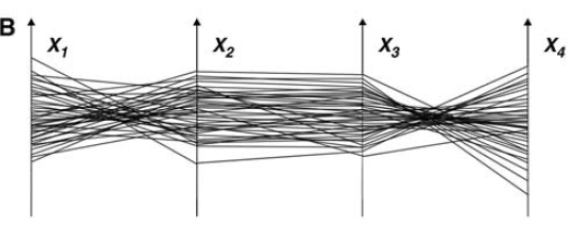
平行坐标系需要的一些问题：

如果太密了看不清楚怎么办？收束捆绑、加不同颜色、颜色变淡……等

4 vis-guide：Graphical Integrity 图形完整性，Lie factor 谎言因素，data-ink ratio

pdf：vis-guide

目的：评价可视化与使用不同的可视化方法

Edward Tufte’s Design Principles 的设计原则

Graphical Integrity 数据的完整性
The lie factor
Maximize data-ink ratio
Avoid harmful chart junk

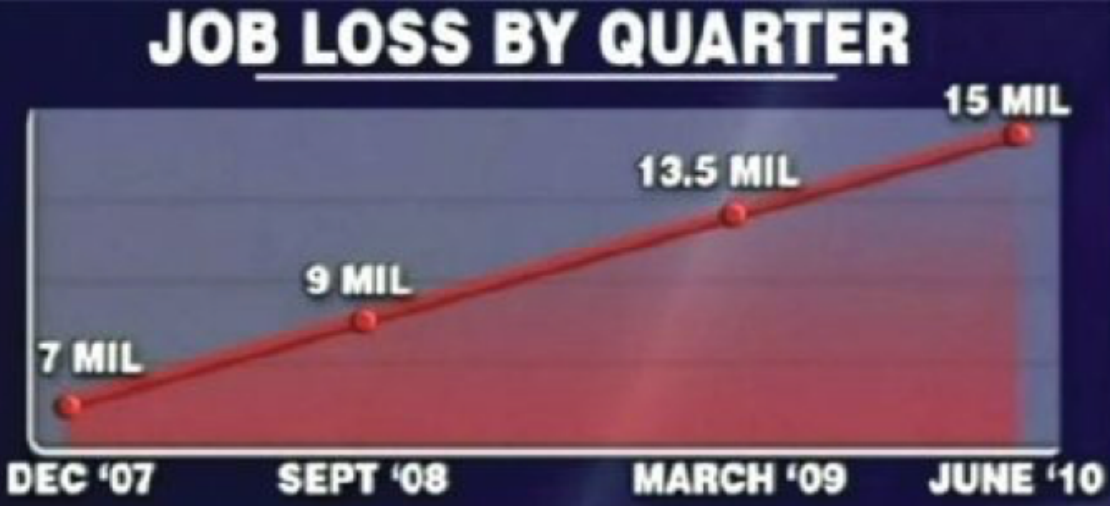
这图的问题：① 横坐标 ② 纵坐标的比例 ③ 标题有误导性

计算 Lie Factor

$ Lie\text{ }Factor = \frac{Size\text{ }of\text{ }effect \text{ }in\text{ }graphic}{Size\text{ }of\text{ }effect\text{ }in\text{ }data} $，$ Size\text{ }of\text{ }effect = \frac{v2-v1}{v1} $

下面这个用面积来表达的，r的平方。

Data-Ink Ratio

用较少的墨水打印更多的数据，但是现在花里胡哨了。

减少chart Junks 比如删掉背景的网格线啊之类的。

Color Maps：颜色不能表示连续性和强弱

5 Color

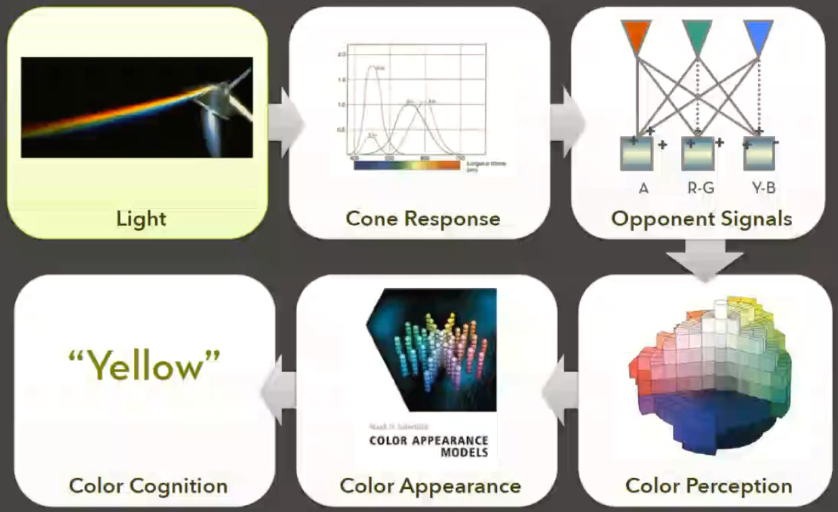
Color perception 的 pipeline，人眼的对于颜色的处理流程

Light -> Cone Response（椎体响应? -> Opponent Signals 对应的信号 -> Color Perception 色彩感知 -> Color Appearance 色彩的外观 -> Color Cognition 色彩认知

Be Wary of Rainbows 它的一些缺点

People segment colors into classes 人们习惯将颜色用于分类/等级
Hues are not naturally ordered 不能表现强度和次序大小最主要的（色调不是自然有序的）
Different lightness emphasizes certain scalar values 翻译：
Low luminance colors (blue) hide high frequencies 高频的值被藏掉了，比如蓝色

**了解一下的：**构造高品质的Color scale、HSV、CLE颜色模型、Color Space

6 Visualization Design Principles; Visual encoding Effectiveness ranking

Design Principles 必须要掌握的，最好用自己的语言可以描述出来

Expressiveness 可表达性
1. A set of facts is expressible in a visual language if the sentences(i.e. the visualizations) in the language express all the facts in the set of data, and only the facts in the data.
2. 能把数据里面的事实表达出来而且仅仅是数据里的事实
3. Tell the truth and noting but the truth (don't lie, and don't lie by omission)
Effectiveness
1. A visualization is more effective than another visualization if the information conveyed by one visualization is more readily perceived than the information in the other visualization.
2. 信息更有效的、更容易的被人感知到，更快和更准确的
3. Use Encodings that people decode better (where better = faster and/or more accurate)

对于不同的量度，影响因素有差别

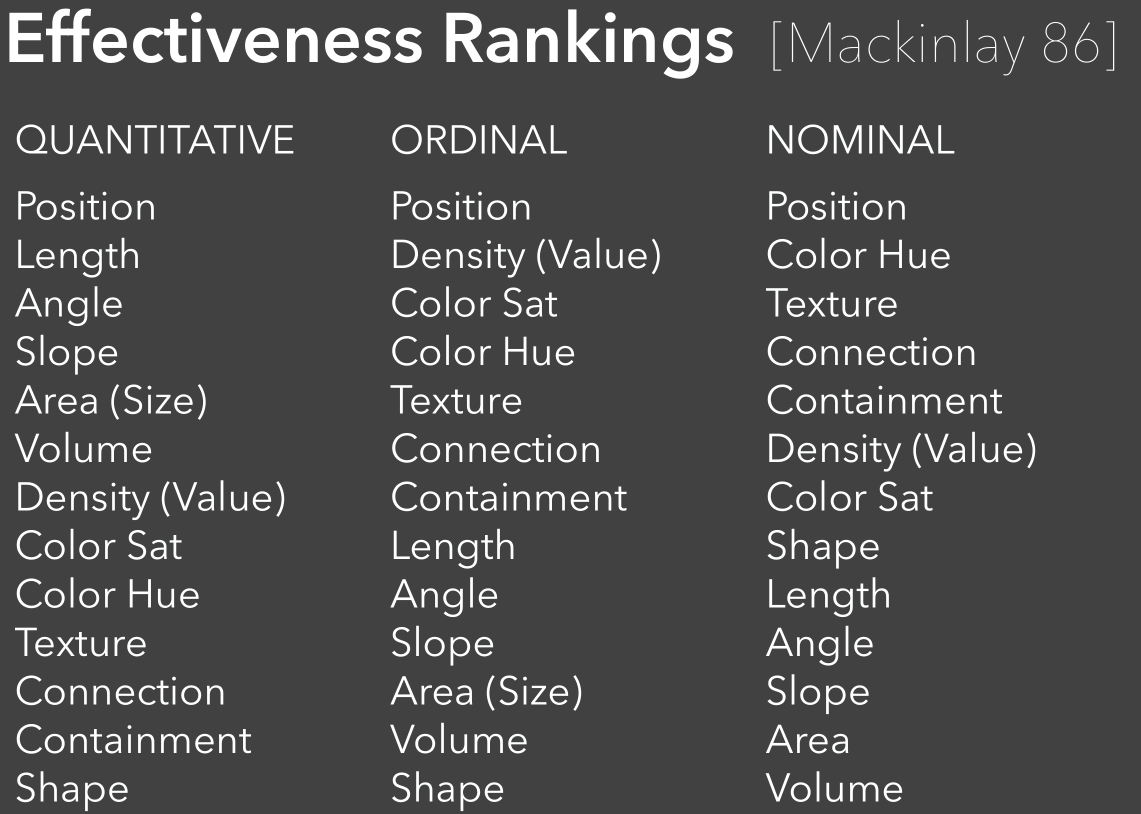
Graphical Perception 的概念

The ability of viewers to interpret visual (graphical) encodings of information and thereby decode information in graphs. Viewers（不一定是人）解释信息编码和在图中解码信息的能力。

**JND - Just Noticeable Difference 的概念 **wiki

最小可觉差， $ {\displaystyle {\frac {\Delta I}{I}}=k, \Delta S= k \frac {\Delta I}{I}} $

$ {\displaystyle I!} $$ {\displaystyle \Delta I! } $k

Gestalt Principles

在格式塔心理学家看来，知觉到的东西要大于眼睛见到的东西；任何一种经验的现象，其中的每一成分都牵连到其他成分，每一成分之所以有其特性，是因为它与其他部分具有关系。由此构成的整体，并不决定于其个别的元素，而局部过程却取决于整体的内在特性。完整的现象具有它本身的完整特性，它既不能分解为简单的元素，它的特性又不包含于元素之内。
格式塔心理学的理论核心是整体决定部分的性质，部分依从于整体。他们通过实验的方式证明感知运动不等于实际运动，也不等于若干的单一刺激，而是与交互作用的刺激网络相关，整体不等于各部分简单相加之和。
“整体不同于其部件的总和”。例如，我们对一朵花的感知，并非纯粹单单从对花的形状、颜色、大小等感官资讯而来，还包括我们对花过去的经验和印象，加起来才是我们对一朵花的感知^[2]。

Figure/Ground 个人理解为负空间、单纯图形线条可以组合出不同的物体
Proximity 相近性，距离相近的各部分趋于组成整体
Similarity 相似性，在某一方面相似的各部分趋于组成整体
Symmetry 对称性，
Connectedness 连接性
Continuity 连续性，
Closure 封闭，
Common Fate Dots moving together are grouped，如果物理沿着相似的光滑路径或具有相似的排列模式，人眼会将它们识别成一类物体。
Transparency 透明度原则，要求图形有连续和适当的色彩。

7 PCA MDS t-SNE

pdf: high-dim-vis, 2DEmbedding

minimize an objective function that measures the discrepancy between similarities in the data and similarities in the map

降维方法小结和理解

PCA

感觉比较好的解释：方差主成分

[简书](https://www.jianshu.com/p/07f4c2356965)

1、去除原始数据的平均值

2、计算原始数据的散度矩阵

3、求解散度矩阵的特征向量和特征值

4、根据特征值的大小，从大到小排序特征向量

5、选取前K个特征向量

6、将原始数据转换到上述K个向量所构建的新空间中完成降维

Metric MDS

[知乎](https://zhuanlan.zhihu.com/p/51441355)

(1)计算原始空间中数据点的距离矩阵。

(2)计算内积矩阵。

(3)对矩阵B进行特征值分解，获得特征值矩阵和特征向量矩阵。

(4)取特征值矩阵最大的前项及其对应的特征向量。

MDS与PCA：

t-SNE

SNE，不同于MDS和ISOMAP中基于距离不变的思想，而是先将欧氏距离距离转换为条件概率，来表达点与点之间的相似度，再优化两个分布之间的距离-KL散度，从而保证点与点之间的分布概率不变。

尽管SNE提供了很好的可视化方法，但是他很难优化，而且存在“拥挤问题”crowding problem。t-SNE在低维空间下使用更重长尾分布的t分布来避免拥挤问题和优化问题。

Crowding问题

拥挤问题就是说各个簇聚集在一起，无法区分。比如有一种情况，高维度数据在降维到10维下，可以有很好的表达，但是降维到两维后无法得到可信映射，比如降维如10维中有11个点之间两两等距离的，在二维下就无法得到可信的映射结果(最多3个点)。进一步的说明，假设一个以数据点xixi为中心，半径为r的m维球(三维空间就是球)，其体积是按rmrm增长的，假设数据点是在m维球中均匀分布的，我们来看看其他数据点与xixi的距离随维度增大而产生的变化。

与SNE的区别，对于q，不再用高斯分布，而是用t分布。

还有一些加速方法。

跟PCA的区别，MDS的区别。

8 Graph Layout force directed, matrix odering

Graph Drawing Aesthetics 画图的美学

Crossings:
1. Minimization of the total crossing number
Area
1. Minimization of drawing area
2. Only meaningful to some layout. Example, grid drawing with integer coordinates
Aspect ratio
1. The ratio of the long and short edge length of its covering rectangle
2. Ideal case is to obtain any aspect ratio in a given range (so the drawing can fit into differently shaped screen space)

Force-Direct Layout of Graph

每个点看做粒子，相互之间引力和斥力，最后达到一个收敛状态。

现在的O(n^3)，起码要掌握O(nlogn)怎么搞，优化策略们。

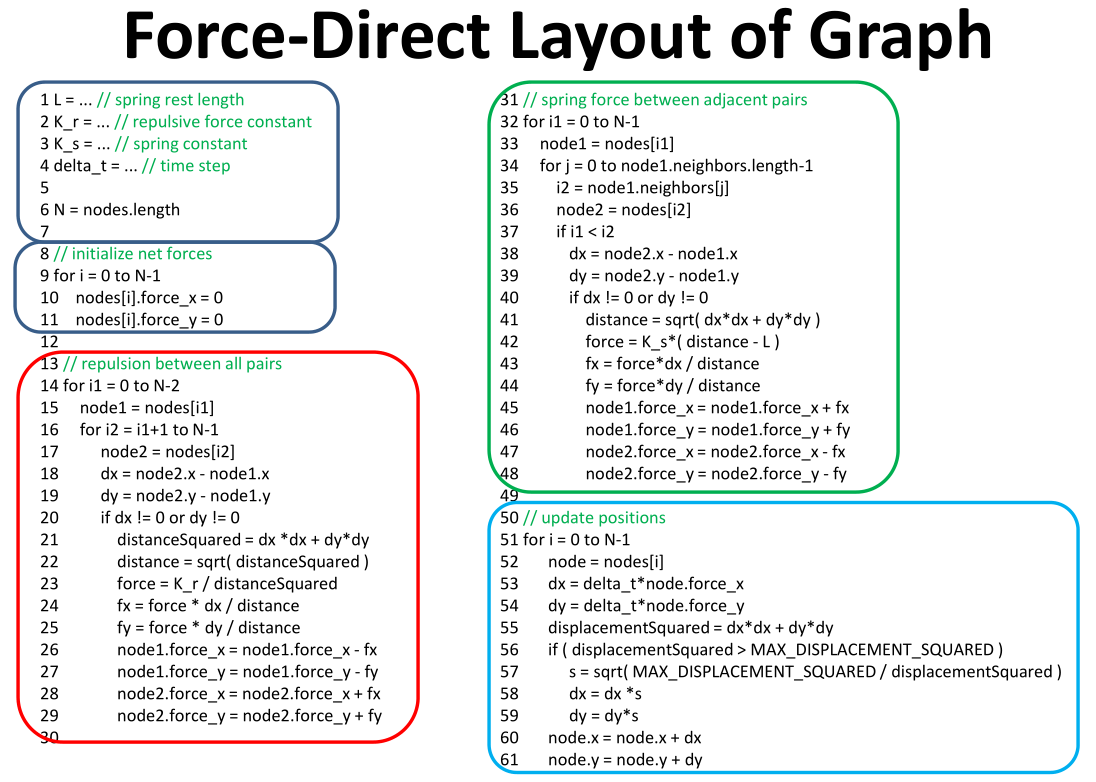
Force-Direct Layout 的缺点

1. Readability: optimization of aesthetic criteria 可读性
2. Scalability: fast computation 可扩展性
3. Visual complexity: interaction tools that allow users to limit the amount of information displayed on the screen 视觉/交互的复杂性性
    1. overview of the graph
    2. details on demand
    3. user’s mental map preservation

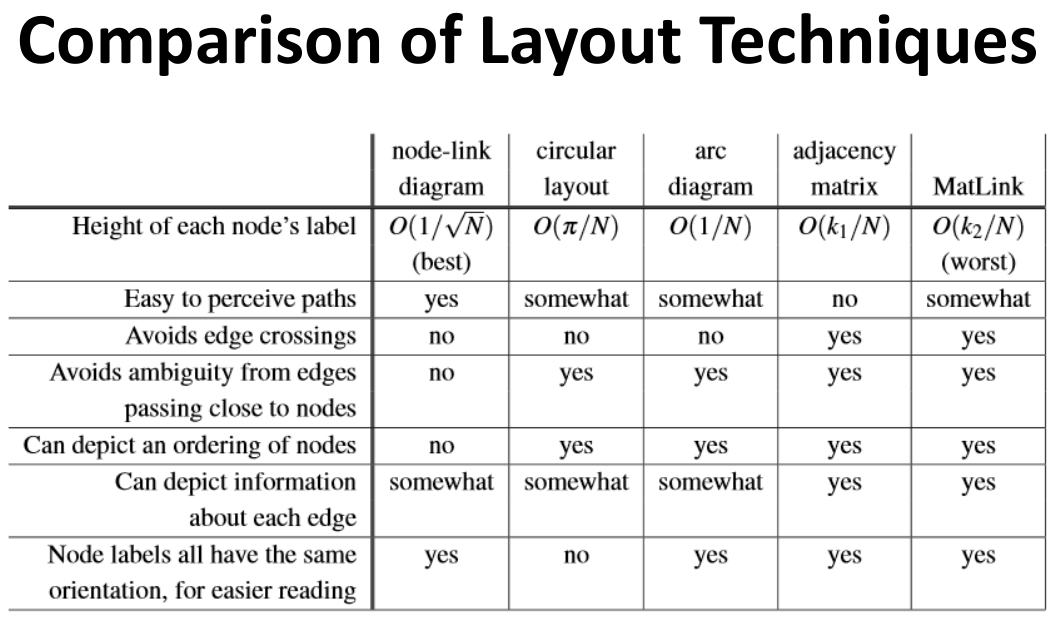
Adjacent Matrix Representations 邻接矩阵存在的一些问题

不同的ordering对它的影响非常大

不同Layout之间的比较

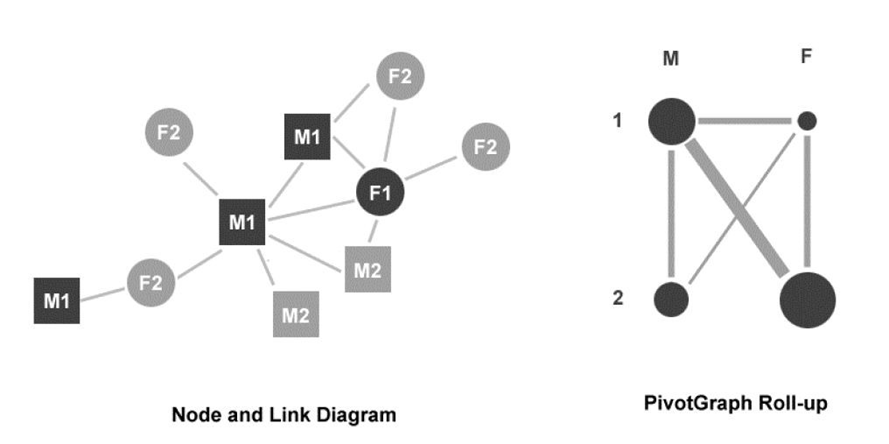
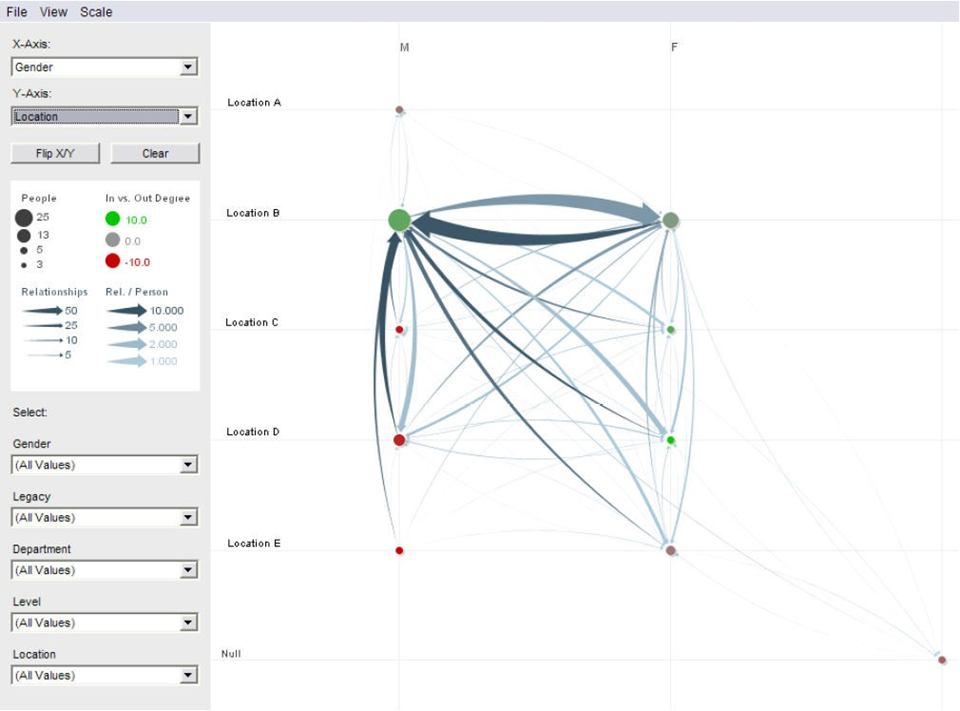
PivotGr****aph 的绘制和解释

Layout aggregate graphs using node attributes. 使用节点属性布局

9 Tree

Reingold-Tilford Layout

实现+内部细节

Goal: make smarter use of space, maximize density and symmetry.

聪明的利用空间，最大化对称性和密度。

需要考虑的设计：

encode depth level No edge crossings 设计深度，无交叉边
Isomorphic subtrees drawn identically 同形子树的画法相同
Ordering and symmetry preserved 保持有序和对称性
Compact layout (don’t waste space) 紧凑的布局

设计步骤：

Initial bottom-up (post-order) traversal of the tree
1. Y-coordinates based on tree depth
2. X-coordinates set piecemeal via “shifts” at each depth
At each parent node: merge left and right subtrees
1. Shift right subtree as close as possible to the left
2. Computed efficiently by maintaining subtree contours
3. “Shifts” in position saved for each node
4. Parent nodes centered above children
Final top-down (pre-order) traversal to set X-coordinates
1. Sum initial layout and aggregated shifts

Treemap Alogrithm

slicing

plain

Draw() {
    Change orientation from parent (horiz/vert)
    Read all files and directories at this level
    Make rectangle for each, scaled to size
    Draw rectangles using appropriate size and color
    For each directory {
    	Make recursive call using its rectangle as focus
    }
}

Squarified Treemaps 的算法不要求，好处需要掌握 Posited Benefits of 1:1 Aspect Ratios ：

Minimize perimeter,reducing border ink. 减少周长和border ink
Easier to select with a mouse cursor. 容易被选择
Similar aspect ratios are easier to compare. 容易比较，但是极端的也并不好。

10 Text

text-doc-vis.pdf

Pipeline

分两个层次

Macro-level
Micro-level

**几种可视化方法：**Themescape、TopicLens、ThemeRiver、Sparkclouds、Wordclouds、Word Tree、ParallelTag Clouds

11 交互 interaction

2020-10-210Interaction.pdf

Interaction between people and machines requires mutual intelligibility or shared understanding.

了解可视化里interaction有哪些

需要掌握：

Overview+ Detail

49页是什么：多视图，同一份数据但是不同的展现形式，比如分辨率的不同，用户可以选择，然后我们把细节展现。

我们需要：Details-on-Demand (DoD)

Provide a viewer with more information and details about a data case(s).

− Get more information about a specific case

− May cause change from an aggregation view to an individual view

Zoom in may result in not all data shown Or data may be abstracted

为浏览者提供能多特定的案例信息，可能会导致从集合视图到个人视图的变化。放大后可能会导致无法显示所有数据，或者数据可能会被抽象化。

Focus + Context

基本理念：The basic idea with focus–plus–context–visualizations is to enable viewers to see the object of primary interest presented in full detail while at the same time getting a overview–impression of all the surrounding information — or context — available. 使Viewers看到感兴趣的部分的全部细节，而且能够看到周围信息/上下文的整体印象。

Three premises 三个前提：

The user needs both overview (context) and detail information (focus) simultaneously. 用户需要同时知道
Information needed in the overview may be different from that needed in detail. 概览与细节包含不同信息。
These two types of information can be combined within a single (dynamic) display, much as in human vision. 这两类信息可以结合在一起。

F+C vs. O+D

一个是 two windows 一个是 merged

Linking and Brushing

不同图之间选择部分的统一性，怎样进行关联。

附录题型

7个简答题 + 2个画图题 + 1个开放题目

更新: 2021-01-10 14:00:32
原文: https://www.yuque.com/qer233/sdu_note/vis

可视化 ​

1 可视化定义，与图形学、数据挖挖掘的关系 ​

2 辛普森悖论 boxplots ​

3 平行坐标系 ​

4 vis-guide：Graphical Integrity 图形完整性，Lie factor 谎言因素，data-ink ratio ​

5 Color ​

6 Visualization Design Principles; Visual encoding Effectiveness ranking ​

7 PCA MDS t-SNE ​

8 Graph Layout force directed, matrix odering ​

9 Tree ​

10 Text ​

11 交互 interaction ​

附录 题型 ​

可视化